Partie 12 - Structures de contrôle - les boucles (3/3)

Structures de contrôle : les boucles

Tout d’abord, si vous êtes arrivés jusque-là c’est que vous avez réussi votre premier crackme, bravo 🎊🥳🎉 !

Mais bon, ce n’est pas tout, il nous reste encore du chemin 🏃 ! Reprenons notre programme decimal_to_binaire, nous nous étions arrêtés à la fonction printBin.

Rappels

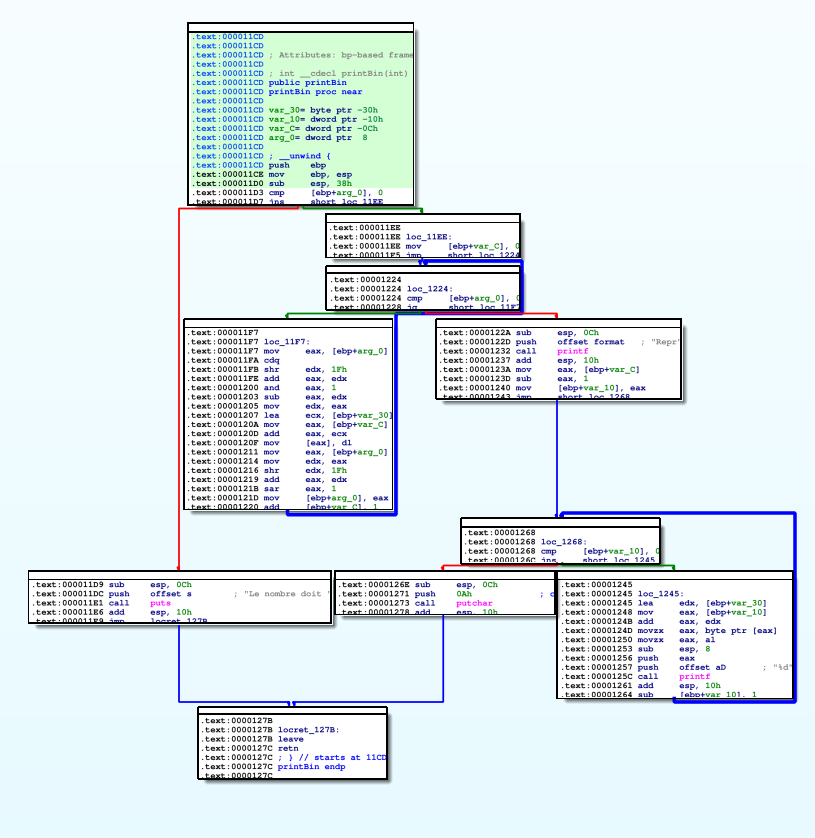
Son graphe a l’allure suivante :

Pour rappel, le code source associé est :

void printBin(int nombre)    
{  
   if (nombre < 0)  
   {  
       printf("Le nombre doit etre un entier positif.\n");  
       return;  
   }  
  
   unsigned char bits[32];    
   int i = 0;  
  
   while (nombre > 0)    
   {  
       bits[i] = nombre % 2;  
       nombre /= 2;  
       i++;  
   }  
  
   printf("Representation binaire : ");  
   for (int j = i - 1; j >= 0; j--)    
   {  
       printf("%d", bits[j]);  
   }  
   printf("\n");  
}

On peut ainsi distinguer, dans le code source, les structures de contrôle suivantes :

• une condition if : vérification su signe
• une boucle while : stockage du nombre bit par bit
• une boucle for : affichage de la représentation binaire bit par bit

C’est pourquoi, comme vous l’avez remarqué, il y a pas mal de blocs dans le graphe désassemblé.

Analyse de la boucle while

Normalement vous ne devriez pas avoir de soucis pour comprendre ce qui se passe jusqu’à l’instruction 1224 cmp [ebp+arg_0], 0 :

1. prologue
2. vérification de l’argument (qui correspond au if du code)
3. initialisation d’une variable locale à 0

Nous avons alors :

cmp     [ebp+arg_0], 0
jg      short loc_11F7

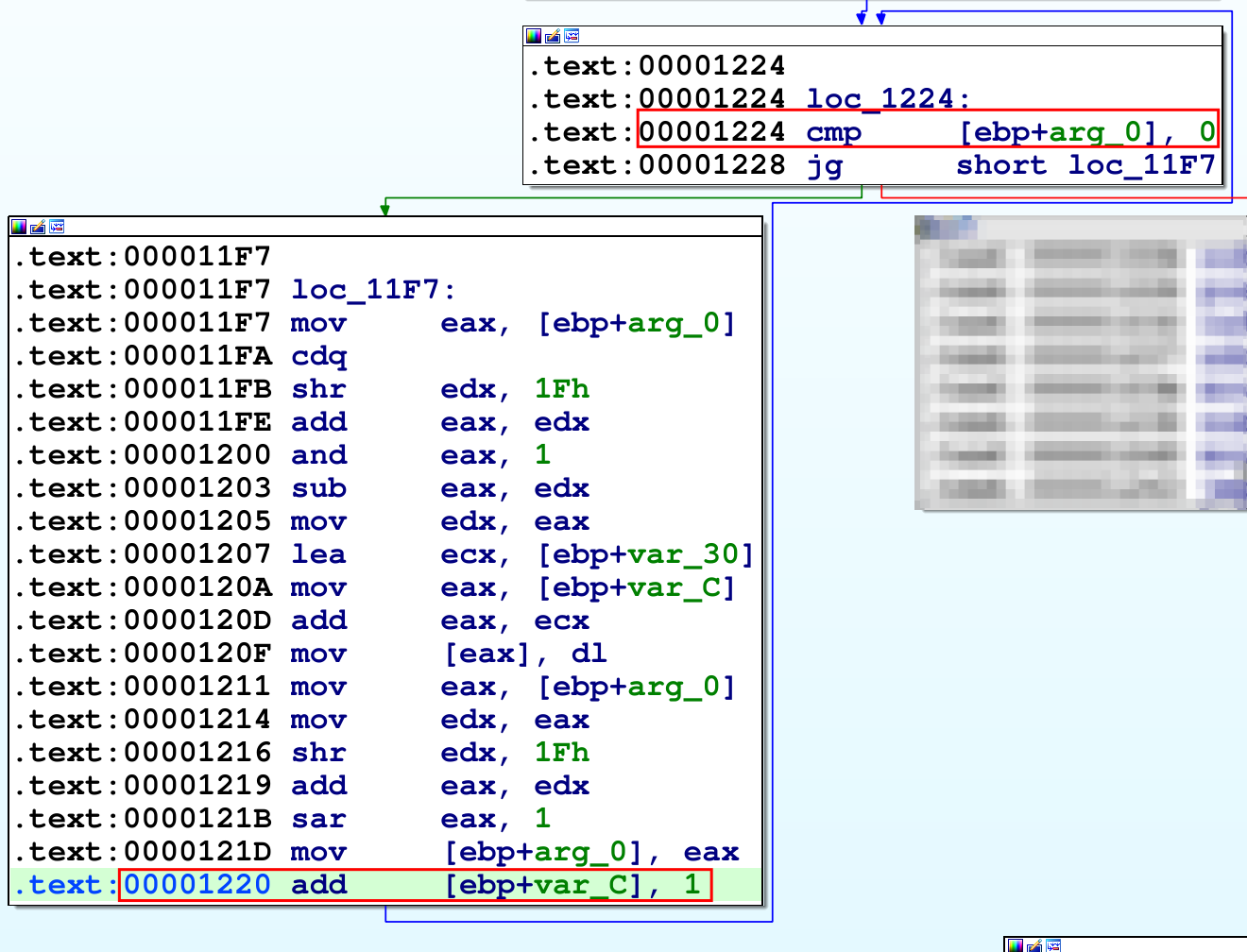
Si l’argument de la fonction est strictement positif, on saute dans le bloc 0x11f7. Pour l’instant, faisons abstraction de ce que contient ce bloc. Intéressons à la manière dont il se finit :

On a l’impression qu’après l’exécution de la dernière instruction du bloc le programme retourne dans le précédent bloc alors qu’il n’y a pas d’instruction de saut, pourquoi ?

En fait si on ouvre bien les yeux, on constate que la fin du second bloc est à l’adresse 0x1220 et que le début du premier est à 0x1224, ce sont donc deux instructions successives ( car la taille de add [ebp+var_C], 1 est de 4 octets). Vous pouvez basculer en mode “texte” pour vous en convaincre. Ainsi, pas besoin de saut.

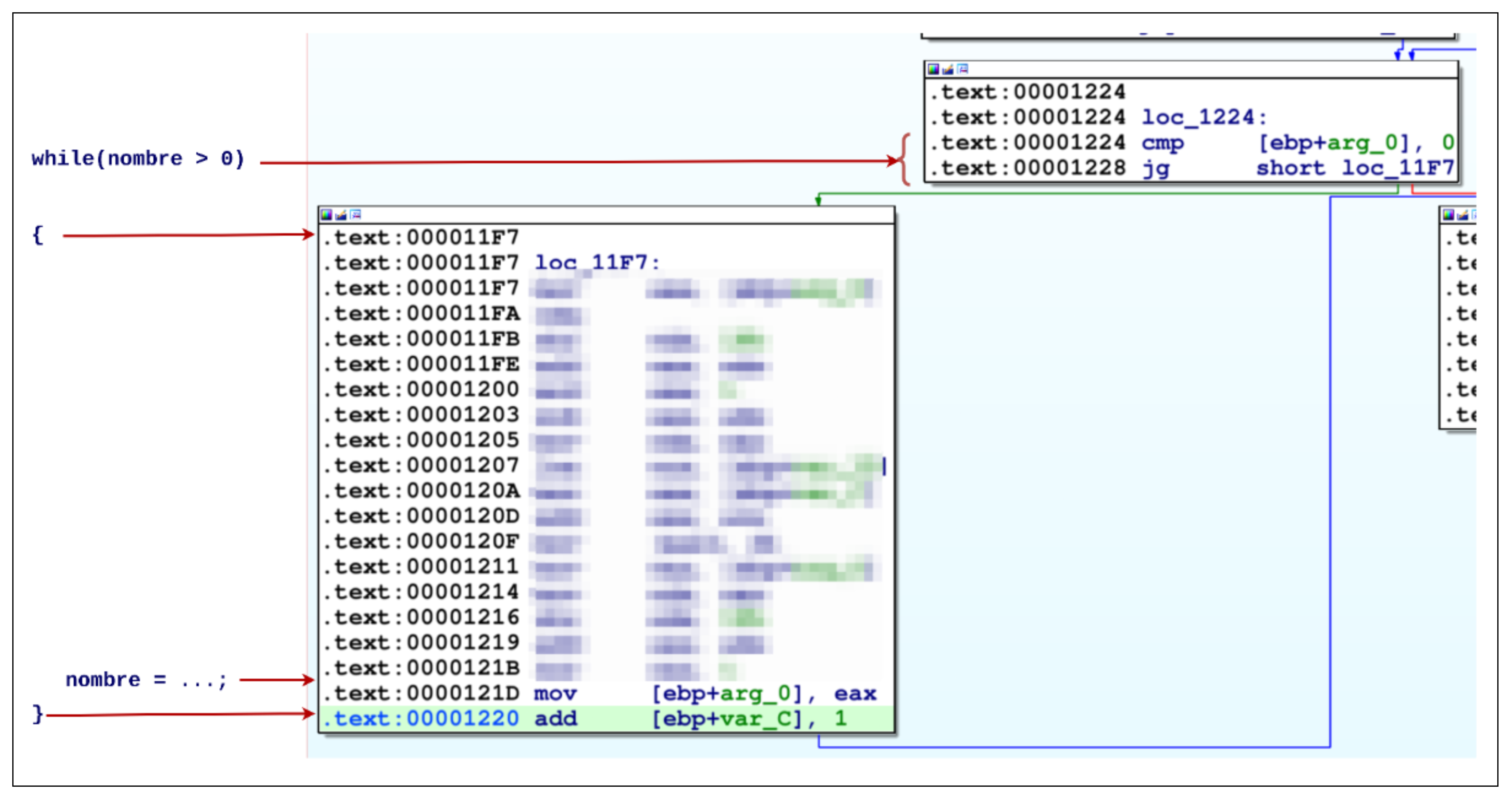
On remarque qu’avant de retourner dans le premier bloc, la valeur de arg_0 est modifiée à 0x1220 : add [ebp+var_C], 1. Finalement, on retrouve bien la structure de notre boucle while :

Bien qu’IDA ait affiché d’abord le bloc de condition avec le bloc contenant le corps de la boucle, dans le code assembleur, le bloc de code (0x11f7) est situé avant le bloc de vérification (0x1224).

Pour ce qui est des boucles do...while, vous l’avez deviné, il suffit (principalement) d’entrer dans le corps de la boucle avant de vérifier la condition de sortie. Sinon, la structure reste semblable à celle d’une boucle while.

Nous n’étudierons pas l’assembleur de la boucle while car cela ne nous permettra pas de mieux comprendre le fonctionnement d’une boucle.

Par contre, vous pouvez analyser son contenu et comparer avec le code source. Cela vous permettra, entre autres, de vous familiariser avec 3 nouvelles instructions que vous pourrez rencontrer dans pas mal de crackmes : cdq¹, shr² et sar.

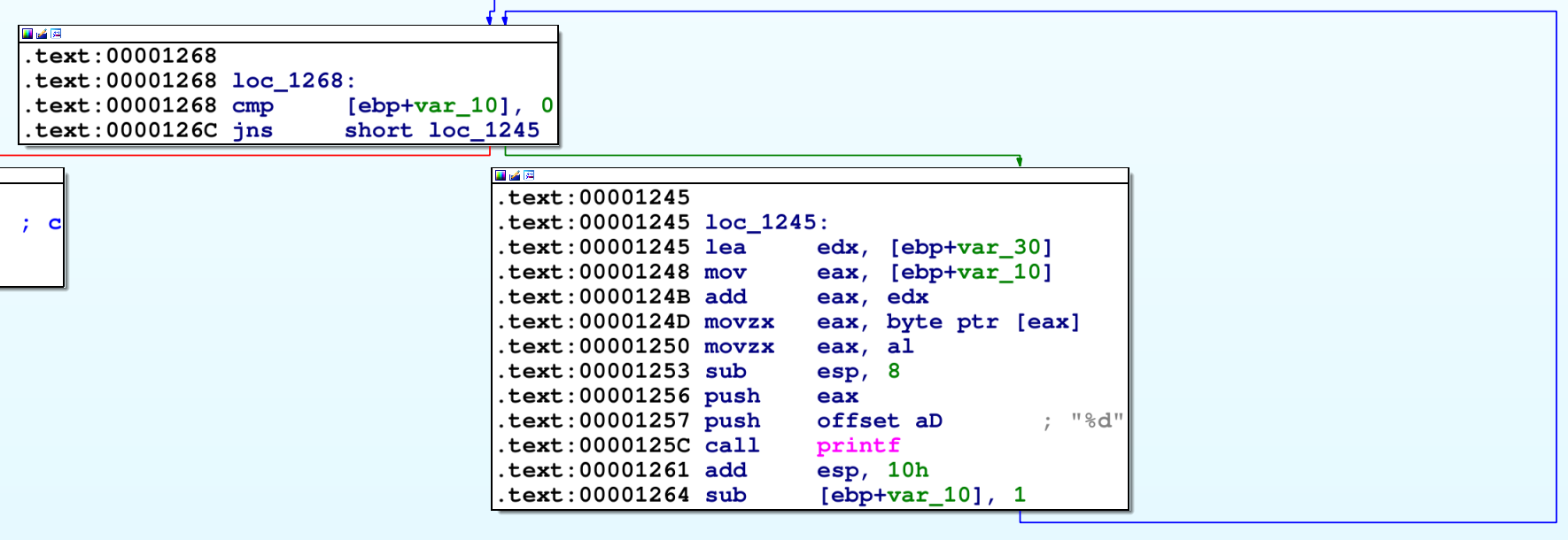
Analyse de la boucle for

La boucle for est ici :

On retrouve exactement la même structure que pour une boucle while. Et puis, on le savait déjà, une boucle for n’est rien d’autre qu’une boucle while plus concise du point de vue d’un développeur :

for(int i = 0; i < N; i++)
{
	// ...
}

// est equivalent a :

int i = 0;
while(i < N)
{
	// ...
	i++;
}

📝 Exercice : analyse d’un switch..case..default

Vous êtes désormais familiers avec les boucles et conditions, on peut alors s’attaquer au switch..case..default.

Mais ! Vous avez l’air d’avoir les connaissances pour comprendre cette structure de code tout seuls 😎 !

Il suffit de faire un petit programme avec un switch, le compiler (sans oublier l’option -m32 pour compiler en 32 bits) et le reverser 🔎 !

Autant la vision “graphe” d’IDA permet de mieux structurer du code assembleur, autant pour comprendre un switch ce n’est pas forcément le plu simple, autant passer en mode “texte”.

📋 Synthèse

Au cours de ces différents chapitres nous nous sommes familiarisés avec les structures de contrôle en assembleur. Ce sont des choses qui nécessitent pas mal de notions sous-jacentes (comparaisons, EFLAGS, sauts conditionnels …) mais qui reviennent tellement souvent dans un programme que vous allez finir par les retenir.

Nous avons notamment vu :

• la manière dont les comparaisons sont réalisées via cmp et test
• les détails des principaux flags utilisés : ZF, SF, CF, OF et PF
• les différents sauts conditionnels : jz, jl, jnb, jg …
• la manière dont les comparaisons et sauts sont utilisés pour réaliser des if/else, while, for …

ℹ️ Instructions mentionnées

1️⃣ L’instruction cdq

Opérandes

• Cette instruction n’a pas d’opérandes

Détails

cdq est l’abréviation de convert dword to qword. Vous l’avez compris, cela devrait donc permettre de convertir un dword (4 octets) en un qword (8 octets), mais comment ?

Tout d’abord, cette instruction ne s’applique que sur le registre eax (ou ses dérivées). C’est pourquoi elle ne dispose pas d’opérandes. De plus, cette instruction garde le signe de l’ancienne valeur lors de la conversion vers la nouvelle valeur.

En x86_64 on a des registres de 64 octets, ce qui n’est pas le cas en x86. Ainsi, pour doubler la taille des données contenues dans eax, c’est le registre edx (ou ses dérivées) qui va être utilisé de cette manière :

• si le nombre dans eax est négatif (bit de poids fort égal à 1), alors edx est rempli de 1
• si le nombre dans eax est positif (bit de poids fort égal à 0), alors edx est rempli de 0

Cette manière de générer une nouvelle valeur à partir d’une valeur signée est ce que l’on appelle l’extension de signe.

Ainsi on obtient une valeur de taille double en concaténant les deux registres sous la forme : edx:eax.

Cette instruction est très utilisée lors des divisions signées afin d’avoir un résultat cohérent et correct.

Exemples

mov eax, 0x70001234
cdq ; edx:eax = 0x00000000:0x70001234

mov eax, 0x80001234
cdq ; edx:eax = 0xffffffff:0x80001234

Équivalent en C

Il n’y pas a pas d’équivalent directe en C.

Autres formes

Il existe plusieurs dérivées mais dont le principe d’extension de signe est le même :

• cwd (convert word to dword): la valeur convertie est contenue dans dx:ax
• cqo (convert qword to double qword): la valeur convertie est contenue dans rdx:rax (disponible seulement en x86_64)

2️⃣ Les instructions shr ope_d, n et sar ope_d, n

Opérandes

• ope_d : opérande de destination. Peut être :
  • un registre
  • un pointeur
• n : opérande source. Peut être :
  • une valeur immédiate
  • un registre (seulement le registre cl)

Détails

L’instruction shr (ou shift right) permet de réaliser un décalage des bits de ope_d de n bits vers la droite.

Avec l’instruction shr et toutes les autres instruction de shift (décalage), il n’y a pas de rotation des bits sortants.

Il existe d’autres instructions comme ror/rol qui réalise un décalage rotatif des bits. C’est-à-dire que des bits qui sortent, par exemple, par la gauche, “rerentrent” par la droite.

Ainsi, le décalage de 0b01110011 d’un bit vers la droite est 0b00111001.

En fait, lorsqu’il y a un bit sortant, il n’est pas réellement perdu dans la nature : il est sauvegardé dans le flag CF des EFLAGS.

Il existe l’instruction sar (ou shift aritmetic right) est basée sur le même principe de décalage que shr. La seule différence est que sar prend en compte le signe du nombre qui sera décalé.

Ainsi, si le bit de poids fort de ope_d est 1, il sera réinitialisé à 1 après décalage. En fait sar agit en deux temps :

1. exécuter shr
2. si le précédent nombre était signé, mettre le bit de poids fort du résultat à 1

Voir les exemples ci-dessous pour comprendre de quoi il s’agit.

Ces instructions sont très utilisées pour réaliser des divisions par 2 d’un nombre (et dont le reste est dans le flag CF). En effet, le décalage d’un bit vers la droite revient à diviser par 2. Le décalage de n bits vers la droite revient à diviser par 2 puissance n.

Je ne vois pas en quoi décaler d’un bit vers la droite revient à diviser par deux ?

Pourtant c’est bien ce qui se passe lorsque l’on note un nombre en décimal et que l’on le décale d’une unité vers la droite, cela revient à diviser par 10.

Prenons par exemple 213950, en le décalant d’une unité vers la droite on obtient 21395, ce qui revient bien à diviser par 10.

Avec la notation en binaire, c’est la même chose : décaler d’un bit revient à diviser par deux.

Ainsi, sar et shr sont très utilisés pour réaliser des divisions de puissances de 2.

Exemple

    mov eax, 0x80000001   (0b10.....001)
    shr eax, 1 ; eax = 0x40000000 (0b01.....000)
               ; CF == 1
               
    mov eax, 0x80000001   
    sar eax, 1 ; eax = 0xc0000000 (0b11.....000)
               ; CF == 1

Équivalent en C

int x = 0x80000001;
x = x >> 1; // x = 0xc0000000

int y = 0xdeadbeef;
y = y >> 13; // y = 0xfffef56d

Autres formes

De la même manière que shr/sar permettent de réaliser des décalages vers la droite, shl/sal permettent de réaliser des décalages vers la gauche avec le même principe.

A l’instar de la division par puissances de 2 de shr/sar, shl/sal permettent de réaliser des multiplications par puissances de 2 :

• ➡️ shr/sar : division par puissances de 2
• ⬅️shl/sal : multiplication par puissances de 2

Vous pouvez également jeter un œil aux instructions rcl/rcr/rol/ror. Leur fonctionnement de décalage est le même. La principale différence est qu’il y a une rotation des bits sortants.

⤴️ Notes

1. Voir ci-dessus : 1️⃣ L’instruction cdq ↩

2. Voir ci-dessus : 2️⃣ Les instructions shr ope_d, n et sar ope_d, n ↩